Los 6 cigarrillos en full contact de la semana pasada se pueden mejorar con la disposición mostrada en la figura, en la que un séptimo cigarrillo se inserta en un hueco central formado por los demás.
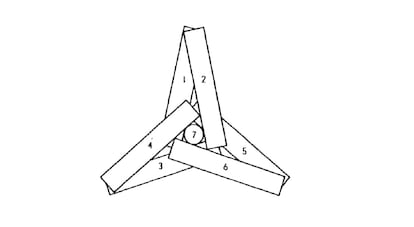
Lo que no se ha demostrado (que yo sepa), es que 7 es el máximo posible (aunque sí se ha demostrado que la solución de la figura no es única, como veremos más adelante).
En cuanto a los cigarrillos —o cilindros— de longitud infinita (la variante la planteó el matemático británico John Littlewood), no han merecido la atención de mis sagaces lectoras/es, pues no han aportado ninguna solución. Aunque tal vez no haya sido una cuestión de atención, sino de dificultad, pues hay que reconocer que no es nada fácil: en la figura se muestra una solución con 6 cilindros, considerada insuperable hasta que, recientemente, se encontraron dos soluciones distintas con 7 cilindros (que, obviamente, lo son también para el caso de los cigarrillos finitos). Observando atentamente la figura, y a partir de ella, tal vez encuentres una de esas soluciones; pero ármate de paciencia, pues, aunque saber que existe facilita las cosas, sigue siendo muy difícil.
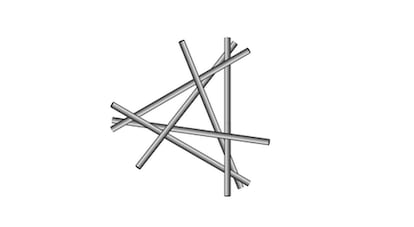
Y pasando de los cilindros rígidos a los flexibles, un problema sencillo para compensar la dificultad de los anteriores:
Tenemos una goma elástica de 1 metro de longitud y una sección circular de 2 mm de diámetro. Si la estiramos hasta que su sección tenga 1 mm de diámetro, y suponiendo que la deformación sea uniforma a lo largo de toda la goma, ¿cuánto mide ahora? Y una vez hallada la solución, intenta “cocinarla”.
La relación entre el estiramiento y el estrechamiento se denomina coeficiente de Poisson, y en la mayoría de los materiales es positivo (a mayor estiramiento, mayor estrechamiento); pero algunos materiales, denominados auxéticos, tienen un coeficiente de Poisson negativo, es decir, se ensanchan al estirarlos.
Los materiales auxéticos sintéticos, como el politetrafluoroetileno expandido (comercializado como Gore-Tex, entre otras marcas), tiene muchas aplicaciones, y, casualmente (aunque en matemáticas y física macroscópica nada es casual), un máximo de hilos (cilindros infinitos, a efectos prácticos) en contacto mutuo está en la base de la fabricación de mallas auxéticas, lo que llevó a los investigadores a buscar ese máximo posible. Que resultó ser 7, según descubrieron antes que los matemáticos.
¿Una pizarra no euclídea?
Las dos chicas de la ilustración principal de la semana pasada no parecen muy duchas en matemáticas, a juzgar por lo que han escrito en la pizarra. Pero no nos apresuremos al juzgarlas: a lo mejor se expresan en términos poco convencionales, pero no por ello erróneos. O tal vez hayan sido objeto de una broma matemática urdida por el mismísimo Lewis Carroll, tan aficionado a desconcertar a las jovencitas con sus aparentes nonsense. ¿Hay alguna posibilidad de que la igualdad 180 = 90 + 30 tenga sentido?
Por otra parte, los ángulos de un triángulo solo suman 180º en el plano euclídeo; sobre otra superficie pueden sumar más o menos de dos rectos (¿puedes dibujar —o describir— un triángulo cuyos ángulos sumen 270º?).
En cuanto al triángulo de la pizarra, sabemos que es rectángulo porque vemos la consabida marca del ángulo oculto, aunque no su valor (solo se ve el 0 final); pero sí que vemos el valor de los agudos: 40º y 30º respectivamente. ¿Es posible darle al ángulo recto oculto un valor que haga que la figura pueda tener sentido?
Y de la ilustración de la semana pasada podemos pasar al texto para plantear un pequeño metaproblema: ¿Qué motivo lógico puede haber para que el corrector automático haya puesto en cursiva el nombre de Poisson, famoso matemático y físico francés?







Comentarios